It is stated as follows :
” The deviation of any point B relative to a tangent drawn to the elastic curve at any other point A in a direction perpendicular to the original position of the beam, is equal to the product of 1/EI and the moment of area about b of that part of the moment diagram between points A and B.”
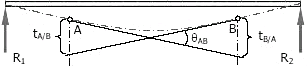
Mathematically it can be written as
![]() Similarly
Similarly
![]()
Where Āb and Āa are the distances from center of gravity of the moment diagram to the point B and A respectively.
For simplification we can say that Ā is the distance from center of gravity of the moment diagram to the point where we have to find deviation.
For instance we are finding the deviation at point B then Ā will be the distance from center of gravity of the moment diagram to the point B, because we are finding deflection at B. Same is the case with any other point such as A.
Leave a Reply